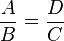SENO COSENO Y TANGENTE DE UN ANGULO

SohCahToa que significa esto???

Sen(del angulo) =opuesto/hipotenusa

Cos(del angulo) =adyacente/hipotenusa

Tan(del angulo) =opuesto/adyacente

renzo gambini 4 "B"

Principio de Arquímedes

En la última experiencia del laboratorio, utilizamos el principio de Arquímides para hallar el volumen de la esfera; pero ¿quíen fue Arquímedes?

Breve Biografía

Arquímedes de Siracusa (c. 287 a. C. – c. 212 a. C.) fue un matemático griego, físico, ingeniero, inventor y astrónomo. Aunque se conocen pocos detalles de su vida, es considerado uno de los científicos más importantes de la antigüedad clásica. Entre sus avances en física se encuentran sus fundamentos en hidrostática, estática y la explicación del principio de la palanca. Es reconocido por haber diseñado innovadoras máquinas, incluyendo armas de asedio y el tornillo de Arquímedes, que lleva su nombre. Experimentos modernos han probado las afirmaciones de que Arquímedes llegó a diseñar máquinas capaces de sacar barcos enemigos del agua o prenderles fuego utilizando una serie de espejos.

Se considera que Arquímedes fue uno de los matemáticos más grandes de la antigüedad y, en general, de toda la historia. Usó el método de exhausción para calcular el área bajo el arco de una parábola con el sumatorio de una serie infinita, y dio una aproximación extremadamente precisa del número Pi. También definió la espiral que lleva su nombre, fórmulas para los volúmenes de las superficies de revolución y un ingenioso sistema para expresar números muy largos.

Arquímedes murió durante el sitio de Siracusa (214–212 a. C.), cuando fue asesinado por un soldado romano, a pesar de que existían órdenes de que no se le hiciese ningún daño.

Eureka

De acuerdo con Vitruvio, Hierón II ordenó la fabricación de una nueva corona con forma de corona triunfal, y le pidió a Arquímedes determinar si la corona estaba hecha sólo de oro o si, por el contrario, un orfebre deshonesto le había agregado plata en su realización. Arquímedes tenía que resolver el problema sin dañar la corona, así que no podía fundirla y convertirla en un cuerpo regular para calcular su masa y volumen, a partir de ahí, su densidad. Mientras tomaba un baño, notó que el nivel de agua subía en la bañera cuando entraba, y así se dio cuenta de que ese efecto podría ser usado para determinar el volumen de la corona. Debido a que el agua no se puede comprimir,la corona, al ser sumergida, desplazaría una cantidad de agua igual a su propio volumen. Al dividir el peso de la corona por el volumen de agua desplazada se podría obtener la densidad de la corona. La densidad de la corona sería menor que la densidad del oro si otros metales menos densos le hubieran sido añadidos. Cuando Arquímedes, durante el baño, se dio cuenta del descubrimiento, se dice que salió corriendo desnudo por las calles, y que estaba tan emocionado por su hallazgo que olvidó vestirse. Según el relato, en la calle gritaba "¡Eureka!" (en griego antiguo: "εὕρηκα" que significa "¡Lo he encontrado!)"

Publicado por Rodrigo Espinoza 4º "B" nº 13

DADO

Un dado es un objeto de forma poliédrica preparado para mostrar un resultado aleatorio cuando es lanzado sobre una superficie horizontal, desde la mano o mediante un cubilete, en cuyo caso los resultados ocurren con distribución uniforme discreta.

Los posibles resultados, numéricos o de otro tipo, están marcados en cada una de las caras del poliedro y se eligen en función de la posición en la que quede el dado tras el lanzamiento; normalmente se toma el resultado marcado en la cara que queda vista hacia arriba. Es frecuente que se utilicen varios dados iguales o diferentes combinados en la misma tirada

HISTORIA

Los dados se consideran derivados de la taba (nombre vulgar del astrágalo de los mamíferos) y de origen asiático. En el texto épico-religioso hindúMahabhárata aparecen menciones del juego de dados.

Fueron también muy usados en Grecia y Roma, como consta por algunas pinturas de vasijas y por los objetos mismos frecuentemente hallados en excavaciones. En Roma se llamaban álea (como dijo Julio César al cruzar el Rubicón: Alea jacta est: ‘el dado tirado está’ o «La suerte está echada». Deálea proviene aleatorio, ‘al azar’.

Aunque generalmente se hacían de marfil o hueso, se encuentran varios de ágata, bronce y vidrio y no faltan algunos fraudulentos que tienen o han tenido relleno de plomo en uno de sus lados. Los romanos designaban todas estas piezas con el nombre de téseras de juego (tésserae lusóriae) pero también llamaban téseras a los billetes de entradas para los teatros y las diferentes clases de bonos y medallas de premios que solían hacerse de metal, marfil o hueso con figuras grabadas.

Dados no cúbicos

En otros tiempos, los dados con formas no cúbicas eran empleados casi en exclusivo por adivinos y en otras prácticas ocultas, por ejemplo en Japón de utilizaba uno con forma de Dodecaedro regular y en cada cara se tenían grabados a los animales del zodiaco chino, el cual se utilizaba en principio como elemento místico y luego pasó a ser un elemento lúdico, pero recientemente se han popularizado en los juegos de rol y wargames. Normalmente, son de plástico y en sus caras hay dígitos en lugar de puntos. Se suelen emplear los sólidos platónicos para fabricar dados de 4, 6, 8, 12 y 20 caras, aunque también se pueden encontrar otras formas para los dados de 10, 30, 100 y otras cantidades de caras, o incluso para los dados antes mencionados.

Se describen con frecuencia por su número de caras de manera abreviada, siendo dX un dado de X caras. Por ejemplo, d6 sería un dado de 6 caras. De forma más general, YdX supone lanzar Y dados, cada uno de los cuales tiene X caras. Para adaptar las puntuaciones disponibles a cierto baremo, se puede añadir una constante al lanzamiento, o multiplicar una tirada por otro número para evitar lanzamientos de un número excesivo de dados. Así, 1d10 + 5significa lanzar un dado de 10 caras y al resultado sumarle 5, mientras que 2 × 3d8 significa tirar tres dados de 8 caras cada uno, y multiplicar el resultado por dos.

Dados trucados

Los dados pueden alterarse de muchas maneras para hacer trampas en los juegos que los requieren: pueden redondearse algunas aristas, algunas caras pueden tener una forma ligeramente distinta a un cuadrado para favorecer la aparición de ciertos resultados. Una manera común es agregar algún material pesado oculto debajo de una de las caras de manera de favorecer un resultado. Los dados empleados en los casinos suelen ser transparentes para dificultar estas maneras de engañar.

por franco kauss perez.4"B"

¿por qué los planetas son esfericos?

Todos los planetas son esféricos debido a sus campos gravitatorios.

Cuando se formaron los planetas, la gravedad juntó billones de piezas de gas y polvo en masas que colisionaron y se calentaron y se sintieron empujadas hacia el centro de gravedad del conjunto.

Los planetas, una vez fríos, siguen comportándose como un fluído a lo largo de extensos periodos de tiempo, sucumbiendo al empuje gravitatorio de su centro de gravedad. El único modo de que toda la masa permanezca lo más cerca posible del centro de gravedad consiste en formar una esfera. El proceso recibe el nombre de ajuste isostático

franco kauss perez 4"B"

ESFERA!

Superficie esférica es la superficie engendrada por una circunferencia que gira sobre su diámetro.

Definición de esfera

Una esfera es la región del espacio que se encuentra en el interior de una superficie esférica.

Elementos de la esfera

Centro

Punto interior que equidista de cualquier punto de la superficie de la esfera.

Radio

Distancia del centro a un punto de la superficie de la esfera.

Cuerda

Segmento que une dos puntos de la superficie esférica.

Diámetro

Cuerda que pasa por el centro.

Polos

Son los puntos del eje de giro que quedan sobre la superficie esférica

Área de la superficie esférica

Volumen de la esfera

Calcular el área y el volumen de una esfera inscrita en un cilindro de 2 m de altura.

Franco Kauss Perez. 4"B"

  

CONO TRUNCADO O TRONCO DE CONO

El cono truncado o tronco de cono es el cuerpo geométrico que resulta al cortar un cono por un plano paralelo a la base y separar la parte que contiene al vértice.

Obtenemos la generatriz del cono truncado aplicando el teorema de Pitágoras en el triángulo sombreado:

AREA LATERAL DE UN CONO TRUNCADO

Área de un cono truncado

Volumen de un cono truncado

}

                                     PUBLICADO POR RENZO               

                                                                   GAMBINI 4B

Trabajo de Campo 1

Bajen el archivo en:

https://sites.google.com/site/peroquefacil/mate-2

Biografia de Tales

Una pequeña ayuda para la tarea del profe Yalta aunque sea muy fácil.

(Mileto, actual Turquía, 624 a.C.-?, 548 a.C.) Filosófo y matemático griego. En su juventud viajó a Egipto, donde aprendió geometría de los sacerdotes de Menfis, y astronomía, que posteriormente enseñaría con el nombre de astrosofía. Dirigió en Mileto una escuela de náutica, construyó un canal para desviar las aguas del Halis y dio acertados consejos políticos. Fue maestro de Pitágoras y Anaxímedes, y contemporáneo de Anaximandro.

Tales de Mileto

Fue el primer filósofo griego que intentó dar una explicación física del Universo, que para él era un espacio racional pese a su aparente desorden. Sin embargo, no buscó un Creador en dicha racionalidad, pues para él todo nacía del agua, la cual era el elemento básico del que estaban hechas todas las cosas, pues se constituye en vapor, que es aire, nubes y éter; del agua se forman los cuerpos sólidos al condensarse, y la Tierra flota en ella. Tales se planteó la siguiente cuestión: si una sustancia puede transformarse en otra, como un trozo de mineral azulado lo hace en cobre rojo, ¿cuál es la naturaleza de la sustancia, piedra, cobre, ambas? ¿Cualquier sustancia puede transformarse en otra de forma que finalmente todas las sustancias sean aspectos diversos de una misma materia? Tales consideraba que esta última cuestión sería afirmativa, puesto que de ser así podría introducirse en el Universo un orden básico; quedaba determinar cuál era entonces esa materia o elemento básico.

Finalmente pensó que era el agua, pues es la que se encuentra en mayor cantidad, rodea la Tierra, impregna la atmósfera en forma de vapor, corre a través de los continentes y la vida no es posible sin ella. La Tierra, para él, era un disco plano cubierto por la semiesfera celeste flotando en un océano infinito. Esta tesis sobre la existencia de un elemento del cual estaban formadas todas las sustancias cobró gran aceptación entre filósofos posteriores, a pesar de que no todos ellos aceptaron que el agua fuera tal elemento. Lo importante de su tesis es la consideración de que todo ser proviene de un principio originario, sea el agua, sea cualquier otro. El hecho de buscarlo de una forma científica es lo que le hace ser considerado como el "padre de la filosofía".

En geometría, y en base a los conocimientos adquiridos en Egipto, elaboró un conjunto de teoremas generales y de razonamientos deductivos a partir de estos. Todo ello fue recopilado posteriormente por Euclides en su obra Elementos, pero se debe a Tales el mérito de haber introducido en Grecia el interés por los estudios geométricos.

Ninguno de sus escritos ha llegado hasta nuestros días; a pesar de ello, son muy numerosas las aportaciones que a lo largo de la historia, desde Herodoto, Jenófanes o Aristóteles, se le han atribuido.

Aristóteles consideró a Tales como el primero en sugerir un único sustrato formativo de la materia; además, en su intención de explicar la naturaleza por medio de la simplificación de los fenómenos observables y la búsqueda de causas en el mismo entorno natural, Tales fue uno de los primeros en trascender el tradicional enfoque mitológico que había caracterizado la filosofía griega de siglos anteriores.

CarlosValdivia Albán 4to "B"

El Teorema de Tales

En la primera experiencia utilizamos el teorema de Tales, pero para los que no les quedó muy claro aquí va en que consiste el teorema.

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, a saber, que:

Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.

Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.
Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.
Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces, del mismo se deduce a modo de corolario que el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande. Esto es, que como por el teorema de Tales ambos triángulos son semejantes, se cumple que:

Este corolario es la base de la geometría descriptiva. Su utilidad es evidente; según Heródoto, el propio Tales empleó el corolario de su teorema para medir la altura de la pirámide de Keops en Egipto. En cualquier caso, el teorema per se demuestra la semejanza entre dos triángulos, no la constancia del cociente.



 Carlos Valdivia Albán 4to "B"

Matemáticas en la Naturaleza

En este Video podemos ver la relación de las matemáticas con la naturaleza, en formas geométricas, la secuencia de Fibonacci, entre otras cosas asombrosas, que vemos en nuestra vida diaria

Rodrigo Espinoza 4ºB

TERCER MILENIO - Luz en Noruega II - OVNIS Pirámide

  por franco Kauss `Perez 4"B"

UN PROBLEMA PARA BRAVOS

Vamos con un problema matematico algo dificil de resolver, ya que solamente las personas que tienen un IQ superior a 120 pudieron resolverlo hasta el momento. Podes utilizar un lapiz y un papel, pero no la calculadora. Luego te doy el resultado.

LOL El primero era un chiste. Ahora paso a mostrarte el problema matematico real.

2 + 3 = 10
7 + 2 = 63
6 + 5 = 66
8 + 4 = 96

Entonces:

9 + 7 = Cuanto es?

DE: Luis Verátegui

IMAGENES CHEVERES

                                                            

DE: Luis Verástegui

UN PROBLEMA MUY FACIL

PERO QUE FACIL ES ESTO...

Con los dígitos: 1, 2, 3, 4 y 5 ¿cuántos números de cinco cifras, sin repetición, se pueden formar?


 a) ¿Cuántos de esos números empiezan por 1?
 b) ¿Cuántos  terminan en  5
 c) ¿Cuántos  empiezan por 1 y acaban en 5?
 d) ¿Cuántos son pares?
 e) ¿Cuántos son múltiplos de 5?
 f) ¿Cuántos son mayores que 20.000?


DE:  Luis Verástegui

La Generatriz

La anterior clase, hicimos ejercicios con la Generatriz, pero la mayoría nos preguntamos qué era...

¿Qué es?

Es una línea recta que genera o engendra una superficie al desplazarse de una forma determinada. 

Si la generatriz es una línea recta conformará una superficie cónica, cilíndrica, etc. Si la generatriz es una cuva, genera esferas, elipsoides, etc. Si se deplaza sobre una o más directrices, genera una superficie reglada.

La generatriz puede ser una línea curva, por ejemplo, una circunferencia que rueda sobre otra circunferencia directriz, tangencialmente. Un punto vinculado a ella describe una trayectora curva que se denomina ruleta cicloidal.

Fórmulas

Generatriz del cilindro

h=g

Generatriz del tronco del cono

g² = h² + (R-r)² 

Generatriz del cono

Generatriz del cono

Generatriz del tronco del cono

Generatriz del cilindro

g² = h² + r<sup>2 

Rodrigo Espinoza, 4º "B"</sup>

Los Politopos

Politopos en la naturaleza

Polígonos

La Calzada del Gigante, en Irlanda

En la naturaleza pueden observarse numerosos polígonos regulares. En el mundo de los minerales, los cristales a menudo tienen caras triangulares, cuadradas o hexagonales. Los cuasicristales hasta pueden tener caras en forma de pentágonos regulares. Otro fascinante ejemplo de polígonos regulares surgidos de procesos geológicos pueden observarse en la Calzada de los Gigantes en Irlanda, o en la Devil's Postpile en California, donde el enfriamiento de la lava ha formado áreas estrechamente acopladas de columnas hexagonales de basalto.

Carambola, una fruta popular del Sureste de Asia.

Los más famosos hexágonos en la naturaleza se encuentran en el reino animal. Los panales de abejas son un arreglo de hexágonos usados para almacenar miel y pólen, así como un lugar seguro para que las larvas crezcan. También existen animales que toman la forma aproximada de polígonos regulares (o al menos tienen la misma simetría); por ejemplo la estrella de mar, y algunas veces otros equinodermos tales como el erizo de mar, muestran la simetría de un pentágono u otros polígonos (tales como el heptágono). De hecho, los equinodermos no muestran simetría radial exacta. Sin embargo, las medusas la presentan, usualmente cuádruple (como el cuadrado) u óctuple.
La simetría radial (y otras simetrías) se observa también ampliamente en el reino vegetal, particularmente entre las flores, y en menor extensión las semillas y las frutas, siendo la formas de simetrí más comunes la pentagonal. Un ejemplo particularmente notorio es el de la carambola (Averrhoa carambola) una fruta semejante al mango originaria del sudeste asiático, cuyo corte seccional tiene forma de una estrella pentagonal.
Moviéndose fuera de la tierra al espacio, los primeros matemáticos realizaron cálculos usando la ley de gravitación de Newton que establece que si dos cuerpos (tales como el Sol y la Tierra) orbitan el uno al otro, existen ciertos puntos en el espacio dónde un cuerpo más pequeño (tal como un asteroide o una estación espacial) permanecerá en una órbita estable, siguiendo por ejemplo a la Tierra pero nunca escapando o "retrasándose". Esos puntos son llamados puntos de Lagrange. El sistema Sol-Tierra tiene cinco puntos Lagrangianos. Los dos más estables están exactamente 60° arriba y detrás de la Tierra en su órbita. Esto es, si trazamos segmentos imaginarios que unan los centros del Sol y de la Tierra y uno de los puntos Lagrangianos estables, formarán un triángulo equilátero. Los astrónomos ya han encontrado asteroides troyanos en esos puntos. Aún se debate la practicidad de instalar una estación espacial en el punto Lagrangiano: aunque podría no necesitar jamás de correcciones de curso, podría tener frecuentemente colisiones con los asteroides que ya están presentes ahí. Existen ya satélites y sondas espaciales en los puntos Lagrangianos menos estables, los que no forman el vértice de un triángulo equilátero con la Tierra y el Sol. Por ahora se han usado sobre todo para la observación solar y la sonda más famos situada en uno de esos puntos ha sido la SOHO.

Poliedros

Los créditos por la primera construcción de sólidos platónicos no corresponden la raza humana. Todos ellos ocurren naturalmente en una forma o en otra, aunque no todas esas ocurrencias son distinguibles a simple vista. El tetraedro, cubo y octaedro aparecen como cristales. No se agotan allí las posibles formas de cristales (Smith, 1982, p 212), de las que hay 48. Ni los icosaedros regulares ni los dodecaedros regulares están entre ellas, aunque una de las formas, el piritoedro (llamado así por el grupo de piritas del cual es típico) tiene doce caras pentagonales, arregladas en el mismo patrón que un dodecaedro regular. Sin embargo, las caras son irregulares, por lo que el piritoedro tampoco es regular.

Circogonia icosahedra, una especia de Radiolaria.

Al inicio del siglo XX, Ernst Haeckel describió (Haeckel, 1904) un número de especies de Radiolaria cuyos esqueletos tienen forma de varios poliedros regulares. Los ejemplos incluyen Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus y Circorrhegma dodecahedra. Las formas de ésas criaturas resultan obvias de sus nombres.
Un descubrimento más reciente es el de un conjunto de nuevos tipos de moléculas de carbono, conocidas como fulerenos (una exposición sencilla de este descubrimiento puede verse en (Curl, 1991)). Aunque C₆₀, el fulereno más fácil de producir, parece más o menos esférico, se supone que algunas de las variedades más grandes (tales como C₂₄₀, C₄₈₀ y C₉₆₀) tienen ligeramente la forma de icosaedros redondeados, de unos pocos nanómetros de diámetro.
Al margen, en tiempos antiguos los pitagóricos creyeron que había una armonía entre los poliedros regulares y las órbitas de los planetas. En el siglo XVII, Johannes Kepler estudió los datos del movimiento planetario compilados por Tycho Brahe y durante una década trató de establecer el ideal pitagoreano encontrando una relación entre los tamaños de los poliedros y los tamaños de las órbitas de los planetas. Su búsqueda fracasó en su objetivo general, pero como consecuencia de estas investigaciones Kepler descubrió que los sólidos que hoy llamamos "de Kepler" son politopos regulares, que las órbitas de los planetas no son círculos, y las leyes del movimiento planetario por las cuales se hizo famoso. En la época de Kepler sólo se conocían cinco planetas además de la Tierra, un número que igualaba el de los sólidos platónicos. El trabajo de Kepler, y los descubrimientos desde ésa época de los planetas Urano, Neptuno y Plutón, han echado por tierra la la idea pitagoreana.

Este artìculo me parecio muy intersante ya que nos de muestra que las figuras geometricas y los poliedros se encuentran constantes en nuestro mundo cotidiano y siempre encontraremos distintas figuros geometricas o algunos poliedros.


Carlos Valdivia Albán